Have you ever wondered about the ancient knowledge that lies hidden in our numerical systems? One such intriguing connection is the Geometric Fibonacci Sequence, a lesser-known variation of the famous Fibonacci Sequence. This sequence not only carries the mathematical beauty and patterns of its predecessor but also holds a deep connection to ancient cultures and their wisdom. In this article, we will explore the fascinating world of the Geometric Fibonacci Sequence and its link to ancient knowledge, from its historical significance to its modern applications. Get ready to delve into the mysteries of numbers and unlock the secrets of the past.
Ancient Numeric Systems
Ancient cultures around the world recognized the profound significance of numbers and their connection to the cosmos. These civilizations developed intricate numeric systems that went beyond mere counting and arithmetic. One famous example is the Babylonian number system, based on the number 60, which gave rise to our modern concept of time division. The Egyptians, on the other hand, used a decimal system that incorporated hieroglyphic symbols to represent different numbers. Another notable numeric system is the Mayan numeral system, known for its use of dots and bars. These ancient numeric systems not only served practical purposes but also had deep spiritual and philosophical meanings. By studying these systems, we gain insights into the ancient knowledge and beliefs that shaped their societies. These numeric systems often found expression in various aspects of ancient cultures, such as architecture and geometry. For instance, the renowned Stonehenge in England is believed to have been built using advanced mathematical calculations. Also, the Golden Ratio, a mathematical proportion derived from the Fibonacci Sequence, can be found in ancient Greek architecture and art. The concept of Sacred Geometry further reveals the connection between mathematics and ancient architecture, highlighting the intricate relationship between numbers, forms, and cosmic harmony. Exploring these ancient numeric systems offers us a glimpse into the wisdom and ingenuity of our ancestors, helping us uncover the secrets of the past and gain a deeper understanding of our present.
The Significance of Numbers in Ancient Cultures
Numbers held great significance in ancient cultures, encompassing both a practical and mystical understanding. Ancient civilizations recognized the inherent power and symbolism behind certain numbers. For example, the number three was often associated with divine trinities or the cycle of life, death, and rebirth. The number seven had a sacred connotation, representing completeness and perfection, observed in the Seven Wonders of the Ancient World and the seven days of the week. Additionally, the number twelve held importance in various cultures, such as the twelve zodiac signs or the twelve tribes of Israel. Numbers were not simply used for counting or measuring, but were imbued with spiritual and cosmological meaning.
Ancient cultures, such as the Egyptians and Mayans, believed that numbers held the key to understanding the mysteries of the universe. Numerology, the study of the occult significance of numbers, played a significant role in their spiritual practices. Numerological calculations were used to determine auspicious dates, interpret dreams, and even predict the future. The Egyptians, in particular, assigned symbolic meanings to different numbers and used them in their funerary rituals, believing that numbers had the power to guide the soul in the afterlife.
Numbers also found expression in ancient architecture and sacred monuments. The construction of structures like Stonehenge is believed to have been influenced by complex mathematical calculations. The positioning of the stones aligns with astrological and solstice events, indicating a deep understanding of celestial patterns and their connection to the earthly realm. The Golden Ratio, a mathematical proportion derived from the Fibonacci Sequence, can be seen in the precise construction of ancient Greek temples and artworks, creating a sense of harmony and beauty.
Numbers held a multifaceted significance in ancient cultures, serving as practical tools for measurement and calculation, while also carrying deep spiritual and symbolic meanings. Exploring the significance of numbers in ancient cultures allows us to gain insights into their belief systems, cosmology, and the profound connection they felt with the universe. By understanding their numerical interpretations, we can unravel the mysteries of the past and appreciate the wisdom passed down through the ages. (source: /sacred-geometry-ancient-architecture/)
Application of Fibonacci Sequence in Ancient Architecture
The application of the Fibonacci Sequence in ancient architecture is a fascinating topic that showcases the remarkable understanding and utilization of mathematical principles by ancient civilizations. One prominent example of this can be seen in the design of the Parthenon, an iconic temple in ancient Greece. The proportions of the Parthenon align with the Golden Ratio, which is closely linked to the Fibonacci Sequence. The Golden Ratio is a mathematical concept where a line or ratio is divided into two parts such that the ratio of the whole line to the longer part is the same as the ratio of the longer part to the shorter part. This ratio, approximately 1.618, is believed to represent aesthetically pleasing and harmonious proportions. In the case of the Parthenon, the dimensions of the temple and its various architectural elements conform to this ratio, creating a visually pleasing and balanced structure. Another example can be found in the positioning of the windows in the Notre-Dame de Paris cathedral. These windows follow a pattern that corresponds to the Fibonacci Sequence, where each window is positioned at a distance equal to the sum of the previous two window placements. This careful arrangement creates a sense of rhythm and balance in the architecture. These examples demonstrate how ancient architects intuitively applied mathematical principles, including the Fibonacci Sequence and the Golden Ratio, to achieve architectural harmony and beauty. By understanding and appreciating these ancient architectural applications, we gain insights into the sophisticated knowledge and advanced skills possessed by these ancient civilizations. To explore further the fascinating mathematics behind ancient structures such as Stonehenge, you can read more about it in our article “Stonehenge: Unraveling the Mathematics” or discover the significance of the Golden Ratio in ancient geometry “The Golden Ratio: Exploring its Role in Ancient Geometry“.
The Fibonacci Sequence

The Fibonacci Sequence is a well-known series of numbers that has captivated mathematicians and intrigued scholars for centuries. It begins with two initial terms, 0 and 1, and each subsequent number in the sequence is the sum of the two preceding numbers. This simple pattern of addition results in mesmerizing and exponential growth. The Fibonacci Sequence has numerous intriguing properties and applications, making it a fascinating subject of study. It is intimately connected to the Golden Ratio, a mathematical proportion renowned for its aesthetic appeal and found extensively in art, architecture, and nature. The sequence also manifests in various natural phenomena, from the arrangement of leaves on plants to the spiraling pattern of shells and the branching of tree limbs. The Fibonacci Sequence appears in unexpected places, such as the stock market, where it influences patterns of growth and decay. Uncovering the historical significance and exploring the mathematical properties of the Fibonacci Sequence offers a captivating journey into the world of numbers and their profound influence on the natural and man-made aspects of our universe.
Understanding the Fibonacci Sequence
To understand the Fibonacci Sequence, we need to dive into the world of mathematics and patterns. The Fibonacci Sequence is a series of numbers in which each number is the sum of the two preceding ones. It begins with 0 and 1, making the third number 1 (0+1=1), the fourth number 2 (1+1=2), the fifth number 3 (1+2=3), and so on. This sequence continues indefinitely, generating a pattern that is deeply rooted in nature and mathematics. The sequence exhibits a unique mathematical property where the ratio of any two consecutive numbers converges towards the golden ratio, approximately 1.61803398875. This ratio is often considered aesthetically pleasing and has been employed in art, architecture, and design throughout history. By understanding the Fibonacci Sequence, we gain insight into the underlying mathematical principles that govern its progression and uncover its significance in various fields of study. Whether it’s found in the spirals of seashells, the branching of trees, or the arrangement of petals in a flower, the Fibonacci Sequence’s presence in nature reveals the intricate interconnectedness and harmony of the natural world. This sequence has been used as a model for population growth, financial analyses, and even in computer algorithms. Through a deeper understanding of the Fibonacci Sequence, we can appreciate the beauty and ubiquity of numbers in our lives and the world around us.
Historical Significance of the Fibonacci Sequence
The historical significance of the Fibonacci Sequence cannot be understated. Although the sequence itself was introduced to the Western world by Leonardo of Pisa, also known as Fibonacci, in the 13th century, its patterns and properties were discovered and utilized by ancient cultures long before his time. In fact, Fibonacci was greatly influenced by the knowledge of the sequence that he encountered during his travels in the Middle East. The Fibonacci Sequence had already been noted in ancient Indian mathematics, with scholars finding equivalent sequences as early as the 6th century. Additionally, Fibonacci discovered that the sequence had already been discussed in ancient Sanskrit poetry, further establishing its historical importance. The Fibonacci Sequence’s presence in ancient cultures hints at its recognition and utilization in various fields, including mathematics, astronomy, art, and architecture. Its appearance in the ancient world is testament to the enduring nature of its mathematical properties and its deep connection to the fundamental principles of the universe. By understanding the historical significance of the Fibonacci Sequence, we gain a greater appreciation for its widespread influence throughout human history and across different cultures.
The Geometric Fibonacci Sequence
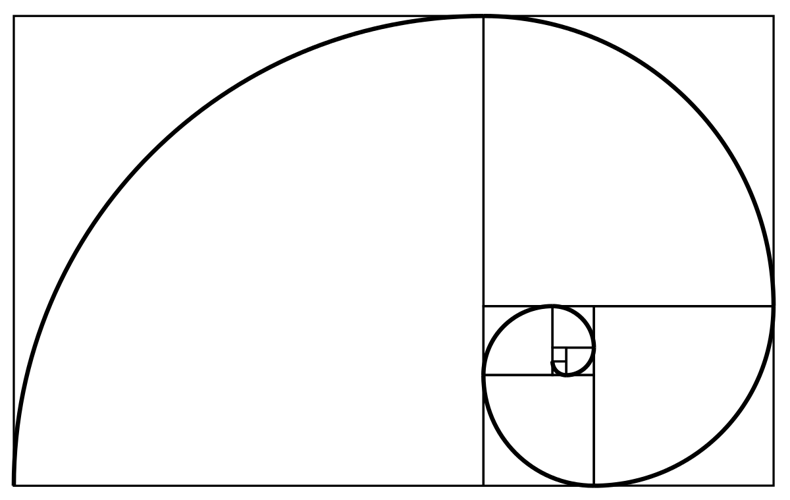
The Geometric Fibonacci Sequence is an intriguing variation of the well-known Fibonacci Sequence that reveals a hidden geometric relationship between its numbers. While the original Fibonacci Sequence follows a linear pattern, the Geometric Fibonacci Sequence introduces a geometric progression into the sequence. In this variation, each number is obtained by multiplying the previous two numbers, resulting in a sequence that expands exponentially. For example, starting with 1 and 1, the sequence would unfold as 1, 1, 2, 2, 4, 8, 32, and so on. This unique geometric aspect adds a new layer of complexity to the sequence, offering a fascinating exploration of mathematical patterns and properties. The Geometric Fibonacci Sequence has intrigued mathematicians and scholars for centuries, as its properties go beyond simple numerical relationships. This sequence has intricate connections to nature, ancient architecture, and even sacred geometry. By delving into the patterns and properties of the Geometric Fibonacci Sequence, we unlock a world of mathematical wonders and uncover the wisdom encoded within its geometric intricacies.
Introduction to the Geometric Fibonacci Sequence
The Geometric Fibonacci Sequence is a fascinating variation of the well-known Fibonacci Sequence that incorporates geometric principles into its structure. This unique sequence combines the mathematical properties of the Fibonacci numbers with the visual and spatial elements of geometric shapes. In the Geometric Fibonacci Sequence, each term is derived by adding the two preceding terms, just like in the original Fibonacci Sequence. However, instead of representing the terms as integers, they are expressed as the areas of squares or the lengths of line segments. This integration of geometry into the sequence adds a new dimension to its patterns and properties.
To better understand the Geometric Fibonacci Sequence, let’s consider an example. We start with two squares, each with an area of 1. We then create a new square with an area equal to the sum of the areas of the previous two squares. This forms the next term in the sequence. Continuing this process, we generate a series of squares where each square’s area is the sum of the areas of the two preceding squares.
The Geometric Fibonacci Sequence exhibits mesmerizing patterns and relationships. For instance, if we draw rectangles around the squares in the sequence, the ratios of the side lengths of these rectangles converge to the golden ratio, approximately 1.618. This mathematical constant is found in various aspects of nature and art, symbolizing harmony and aesthetic balance.
Understanding the Geometric Fibonacci Sequence also allows us to explore its connections to other geometric figures, such as triangles and circles. By constructing geometric shapes based on the sequence’s terms, we discover intricate relationships and intricate patterns that showcase the elegance and mathematical beauty of this sequence.
Next, we will delve deeper into the specific patterns and properties of the Geometric Fibonacci Sequence and its significance in ancient cultures. Brace yourself for a journey into the captivating world where mathematics and geometry intertwine to unlock ancient wisdom and knowledge.
Patterns and Properties of the Geometric Fibonacci Sequence
The Geometric Fibonacci Sequence, as its name suggests, exhibits unique patterns and properties that set it apart from the traditional Fibonacci Sequence. Let’s explore these captivating characteristics:
1. Exponential Growth: Similar to the Fibonacci Sequence, the Geometric Fibonacci Sequence also demonstrates exponential growth. However, instead of adding the previous two terms to obtain the next term, in the Geometric Fibonacci Sequence, each term is multiplied by a common ratio. This ratio, denoted as ‘r’, can be any positive real number.
2. Diverse Ratios: Unlike the fixed ratio of 1.618 found in the Golden Ratio associated with the Fibonacci Sequence, the Geometric Fibonacci Sequence allows for a wide range of ratios to be used. These ratios can be rational or irrational numbers, providing a greater flexibility in exploring mathematical relationships.
3. Spiral Patterns: When the terms of the Geometric Fibonacci Sequence are displayed as points on a coordinate plane and connected sequentially, they form captivating spiral patterns. These spirals can exhibit both clockwise and counterclockwise rotations, depending on the chosen common ratio.
4. Self-Similar Properties: The Geometric Fibonacci Sequence possesses a self-similar nature. This means that when a section of the sequence is isolated, it mirrors the overall structure of the entire sequence. This property allows for fascinating insights into the interplay between individual terms and the larger sequence.
5. Convergence and Divergence: Depending on the value of the common ratio ‘r’, the Geometric Fibonacci Sequence can either converge or diverge. Convergence occurs when the terms approach a finite number, while divergence happens when the terms become infinitely large or small.
Exploring the patterns and properties of the Geometric Fibonacci Sequence offers mathematicians and enthusiasts a rich landscape to study and analyze. Its versatility and unique characteristics make it a captivating subject of investigation, leading to further discoveries and applications in various fields of mathematics and beyond.
Ancient References to the Geometric Fibonacci Sequence
Ancient references to the Geometric Fibonacci Sequence can be found in various cultures and civilizations, showcasing the universality of this mathematical concept. One such reference is in the architecture of the Parthenon, an ancient Greek temple dedicated to the goddess Athena. The dimensions of the Parthenon exhibit a fascinating correlation to the Fibonacci Sequence, with the ratio of the length to the width of the temple being approximately 1.618, the Golden Ratio derived from the Fibonacci Sequence. This ratio was believed to be aesthetically pleasing and harmonious, and its integration into the design of the Parthenon demonstrates the significance ancient Greeks placed on mathematical proportions.
Another notable example of an ancient reference to the Geometric Fibonacci Sequence can be found in the architecture of the Great Pyramids of Egypt. The dimensions of these monumental structures also align with the Fibonacci Sequence, with each subsequent pyramid being approximately 1.618 times larger than its predecessor. This consistent growth ratio is a reflection of the inherent balance and harmony found within the Fibonacci Sequence.
In addition to architecture, ancient references to the Geometric Fibonacci Sequence can be found in artwork and symbolism. For instance, the spiral embellishments seen in ancient Celtic artwork often follow the geometric progression of the Fibonacci Sequence. These spirals reflect the inherent balance and growth found within the sequence, representing the cycle of life and nature’s inherent harmonious design.
Through these ancient references, we can witness the importance placed on the Geometric Fibonacci Sequence by ancient civilizations. It demonstrates the profound understanding and appreciation these cultures had for the inherent mathematical patterns that govern the natural world. By incorporating these patterns into their art, architecture, and symbolism, they sought to embody the harmony and balance found within the Fibonacci Sequence, connecting their physical creations to the underlying principles of the universe.
Ancient Knowledge Encoded

Ancient knowledge was often encoded in various forms, including symbols, texts, and architectural designs, providing a means of transmitting wisdom across generations. One fascinating aspect of this encoded knowledge is its connection to the Geometric Fibonacci Sequence. Sacred Geometry, an ancient practice that explores the inherent harmony and symbolism of geometric shapes, often incorporates the principles of the Geometric Fibonacci Sequence. This sequence is believed to hold profound significance and is found in the designs of sacred sites worldwide, such as the Great Pyramid of Giza and the Parthenon in Athens. These structures not only showcase the mathematical precision of the Geometric Fibonacci Sequence but also serve as repositories of ancient wisdom and spiritual truths. Additionally, ancient texts, such as the Egyptian Book of the Dead and the Hindu Vedas, contain references to the sequence, suggesting a deeper understanding of its cosmic significance. By unraveling the encoded messages within these ancient texts and symbols, we can gain insights into the profound connections between mathematics, spirituality, and the fundamental fabric of the universe.
Sacred Geometry and the Geometric Fibonacci Sequence
Sacred Geometry and the Geometric Fibonacci Sequence are intertwined in their remarkable connection to the divine and the natural world. Sacred Geometry is the study of geometric shapes and patterns that hold symbolic and spiritual significance. Many ancient civilizations believed that certain geometric forms had inherent power and were expressions of the divine order in the universe. The Geometric Fibonacci Sequence, on the other hand, builds upon the traditional Fibonacci Sequence by incorporating geometric shapes and patterns. It is a sequence where each term represents the sum of the previous two terms, but instead of using numbers, it utilizes geometric elements such as squares, triangles, and circles.
One of the most well-known examples of the fusion between Sacred Geometry and the Geometric Fibonacci Sequence is the golden spiral. This spiral is derived from the ratios found within the Fibonacci Sequence and manifests in numerous natural phenomena, such as the growth patterns of shells, hurricanes, and even the arrangement of seeds in flowers. The golden spiral is believed to embody harmony and balance, and it is often associated with the divine proportion known as the golden ratio.
The golden ratio is a mathematical ratio of approximately 1.618, and it has been revered for its aesthetic appeal and perceived perfection. In Sacred Geometry, the golden ratio is seen as a fundamental building block, representing a harmonious relationship between different elements. It is believed that the presence of this ratio in various architectural and artistic compositions creates a sense of beauty and harmony that resonates with the viewer on a profound level.
In ancient temples, cathedrals, and sacred spaces, the principles of Sacred Geometry and the Geometric Fibonacci Sequence were often employed to create spaces that induce a sense of awe and spiritual connection. The dimensions, proportions, and alignments of these structures were carefully calculated to align with cosmic energies and produce sacred vibrations. The intricate patterns and symmetries found within these sacred spaces reflect the divine order that ancient cultures believed governed the universe.
Symbols such as the Flower of Life, the Seed of Life, and the Vesica Piscis are often associated with Sacred Geometry and the Geometric Fibonacci Sequence. These symbols represent the interconnectedness of all creation and signify the source of life and evolution. They can be found in ancient texts, artwork, and architectural designs, serving as guides to tap into the profound wisdom encoded within the geometric patterns.
In essence, Sacred Geometry and the Geometric Fibonacci Sequence offer a deep understanding of the interconnectedness and sacredness of the natural world. They provide a framework through which we can explore the divine order and find spiritual meaning in the mathematical patterns that underlie our universe. By recognizing and studying these principles, we can gain a greater appreciation for the intricate beauty that surrounds us and tap into ancient wisdom that has been passed down through the ages.
Ancient Texts and Symbols Connecting to the Geometric Fibonacci Sequence
Ancient texts and symbols have been discovered that suggest a deep connection between the Geometric Fibonacci Sequence and the wisdom held by ancient civilizations. One such example is the use of the Golden Rectangle in ancient artwork and architecture. The Golden Rectangle, which is derived from the Fibonacci Sequence, exhibits perfect geometric proportions that were believed to represent harmony and balance in the ancient world. This can be seen in the construction of structures like the Parthenon in Athens, where the dimensions of the building and its decorative elements adhere to the Golden Ratio. Similarly, ancient texts from cultures such as the Egyptians and the Mayans contain references to numerical sequences and proportions that bear striking resemblance to the Fibonacci Sequence. These texts often contain instructions for creating sacred structures and objects with specific dimensions, emphasizing the significance of mathematical relationships in their cultural and religious practices. The presence of these ancient texts and symbols further reinforces the idea that the Geometric Fibonacci Sequence held a special place in the knowledge and understanding of ancient civilizations, connecting them to the profound principles of harmony, balance, and hidden cosmic order.
Ancient Wisdom Embedded in the Geometric Fibonacci Sequence
Ancient wisdom is intricately woven into the fabric of the Geometric Fibonacci Sequence, providing us with profound insights into the beliefs and knowledge of past civilizations. One fascinating aspect of this connection lies in the use of the sequence in ancient texts and symbols. For example, in the ancient Indian text known as the Chandahśāstra, the Geometric Fibonacci Sequence is described as a reflection of divine order and cosmic balance. Similarly, ancient Egyptian hieroglyphs depict patterns that align with the sequence, indicating its importance in their understanding of the universe. Ancient symbols such as the Awen, found in Celtic cultures, closely resemble the spirals found within the Geometric Fibonacci Sequence, suggesting a shared understanding of sacred geometry and its connection to the natural world. These ancient references highlight the universality of the sequence as a representation of harmonious growth and divine proportions.
Beyond textual and symbolic references, the Geometric Fibonacci Sequence also reveals ancient wisdom through its inherent mathematical properties. The sequence’s spiral pattern, as demonstrated in the famous Fibonacci Spiral, reflects the growth patterns found in nature, such as the arrangement of seeds in a sunflower or the branching of trees. This organic connection to the natural world emphasizes the ancient belief in the interconnectedness of all living things and the presence of a divine order underlying creation.
Additionally, ancient cultures utilized the sequence in their architectural designs, incorporating its ratios and proportions to create buildings and structures that were not only aesthetically pleasing but also harmoniously aligned with the surrounding environment. This integration of the Geometric Fibonacci Sequence into ancient architecture demonstrates a deep understanding of the mathematical principles that govern beauty and balance, serving as a testament to the advanced knowledge and wisdom of civilizations past.
By unraveling the ancient wisdom embedded in the Geometric Fibonacci Sequence, we gain a profound appreciation for the deep-seated connections between mathematics, spirituality, and the natural world. It serves as a reminder that our ancestors held a deep reverence for the universal principles that govern our existence and sought to represent them in their art, architecture, and philosophical teachings. Exploring these ancient connections allows us to tap into a wellspring of wisdom that continues to resonate with us in the present day.
Modern Applications and Discoveries
The Geometric Fibonacci Sequence continues to captivate mathematicians and researchers today, as its applications reach far beyond ancient civilizations. In nature, the sequence can be observed in the arrangement of petals in flowers, the branching patterns of trees, and even the spirals found in shells and hurricanes. These natural occurrences demonstrate the inherent beauty and efficiency of the sequence, inspiring modern designers, architects, and artists. Additionally, the Geometric Fibonacci Sequence has found its place in various fields of modern mathematics, including number theory, graph theory, and fractal geometry. Mathematicians continue to explore and unravel the mysteries embedded within this sequence, using it to solve complex problems and discover hidden patterns. From cryptography to computer science, the applications of the Geometric Fibonacci Sequence continue to push the boundaries of knowledge and offer new insights into the intricate fabric of the universe. Its versatility and presence in both the natural world and mathematical systems make it a valuable tool for exploration and innovation in modern times.
The Geometric Fibonacci Sequence in Nature
The Geometric Fibonacci Sequence, with its unique properties and patterns, can be observed not only in the realm of mathematics but also in the natural world around us. Nature is filled with examples that showcase the presence of the Geometric Fibonacci Sequence, serving as a testament to its prevalence and significance. One notable instance is found in the spirals and patterns of various plants. The arrangement of leaves, petals, and seeds often follows the sequence, with each new element appearing at a distance or angle based on the Fibonacci numbers. This can be observed in the perfect symmetry of a sunflower’s seeds spiraling outwards or in the petals of a rose forming spirals according to the sequence. In addition to plants, the Geometric Fibonacci Sequence also appears in the growth patterns of seashells and the shape and arrangement of pinecones. It is the inherent relationship between mathematics and the natural world that allows for the presence of these geometric patterns. By studying and understanding the Geometric Fibonacci Sequence in nature, scientists and researchers are able to unravel the mysteries of growth and formation, gaining insights into the beautiful patterns and intricate designs that surround us. The fascinating connection between mathematics and the natural world serves as a reminder of the inherent harmony and order present in our universe.
Applications of the Geometric Fibonacci Sequence in Modern Mathematics
The Geometric Fibonacci Sequence, with its unique properties and connections, has found numerous applications in modern mathematics. One prominent application is in the field of number theory, where the sequence is studied to understand the distribution of prime numbers. Researchers have explored patterns within the sequence to uncover clues about the occurrence and behavior of prime numbers, leading to advancements in prime number theory.
Another area where the Geometric Fibonacci Sequence has proven valuable is in mathematical modeling. By incorporating the patterns and ratios present in the sequence, mathematicians have been able to develop models that accurately represent various natural phenomena. For example, the growth patterns of certain plants, the spiral formations in seashells, and the arrangement of leaves on a stem can all be modeled using the principles of the Geometric Fibonacci Sequence. This has provided insights into the inherent order and harmony found in nature.
Additionally, the sequence has found applications in computer science and data analysis. Its recursive nature and self-repeating patterns make it an ideal tool for generating random-like numbers for simulations and encryption algorithms. It has also been used in image compression techniques to efficiently store and transmit visual data.
The Geometric Fibonacci Sequence is an essential component in the field of fractal geometry. Fractals are complex structures that exhibit self-similarity at different scales, and the sequence is often involved in the generation and calculation of fractal patterns. Fractals have applications in diverse fields such as computer graphics, terrain modeling, and the study of chaotic systems.
The Geometric Fibonacci Sequence plays a significant role in modern mathematics with numerous applications across various disciplines. Its properties have been harnessed to study prime numbers, model natural phenomena, develop encryption algorithms, and explore fractal geometry. The sequence’s versatility and wide-ranging applications continue to inspire further research and innovation in the field of mathematics.
Unraveling Mysteries with the Geometric Fibonacci Sequence
The Geometric Fibonacci Sequence has become a powerful tool in unraveling mysteries across various fields of study. One fascinating area where this sequence has made significant contributions is in the exploration of natural phenomena. Scientists and researchers have discovered the presence of the Geometric Fibonacci Sequence in various aspects of nature, from the arrangement of leaves on plants to the spirals found in seashells and galaxies. The spiral patterns created by the sequence, known as logarithmic spirals, can be seen in the growth patterns of sunflowers and pinecones. These natural occurrences reflect the inherent order and harmony present in the Geometric Fibonacci Sequence, unlocking the secrets of growth and symmetry in nature.
Beyond the realm of biology, the Geometric Fibonacci Sequence has also found applications in modern mathematics. Mathematicians have utilized the sequence to solve complex problems and explore patterns in number theory, geometry, and algebra. The relationship between the Fibonacci Sequence and the Golden Ratio has been extensively studied, showcasing the interconnectedness of these mathematical concepts. The Golden Ratio, often represented by the Greek letter φ (phi), is derived from the ratio of consecutive Fibonacci numbers and holds remarkable aesthetic and proportional properties. Its presence can be observed in various forms of art, architecture, and design throughout history, exemplifying the timeless appeal of the Geometric Fibonacci Sequence.
The Geometric Fibonacci Sequence continues to unravel mysteries in diverse fields such as computer science, finance, and cryptography. Its unique properties and elegant patterns provide a foundation for developing algorithms, analyzing market trends, and encrypting information. The sequence’s inherent balance and efficiency make it a valuable tool for solving complex problems and unlocking hidden patterns in data.
The Geometric Fibonacci Sequence holds the key to unraveling mysteries in both the natural world and the realm of mathematics. Its presence in nature showcases the underlying order and harmony embedded in the universe. Meanwhile, its applications in various mathematical disciplines and practical fields contribute to advancements in science, technology, and human knowledge. As we continue to explore the mysteries of the Geometric Fibonacci Sequence, we unlock new insights into the fundamental principles that govern our world.
Conclusion
In conclusion, the Geometric Fibonacci Sequence serves as a remarkable bridge between ancient knowledge and modern understanding. Its connection to ancient cultures, architecture, and sacred geometry showcases the profound wisdom embedded in numerical patterns. Through the study of this sequence, we not only gain insight into the historical significance of numbers but also witness their enduring influence in various fields of study. From the mathematical beauty of the Fibonacci Sequence to the geometric variations that extend its patterns, the Geometric Fibonacci Sequence offers a unique perspective on the intricate relationship between mathematics and the natural world. Moreover, the ancient references and encoded knowledge hint at a deeper understanding of the universe and our place within it. As modern researchers continue to unravel the mysteries behind this sequence, new discoveries are made, shedding light on the secrets of the past and paving the way for future advancements. The Geometric Fibonacci Sequence is a testament to the timeless nature of knowledge, transcending cultures and time periods. It challenges us to explore the boundaries of human understanding and seek deeper connections in the pursuit of knowledge and wisdom.
Frequently Asked Questions
What is the significance of numbers in ancient cultures?
Numbers held great significance in ancient cultures, representing various aspects of life, spirituality, and the cosmos. They were believed to possess mystical properties and were used in divination, astrology, and religious rituals.
How was the Fibonacci Sequence used in ancient architecture?
The Fibonacci Sequence, with its inherent ratios and patterns, was believed to create aesthetically pleasing proportions in architecture. It was used to design structures that harmonized with the natural world, such as the Parthenon in Athens and the pyramids of Egypt.
What is the Geometric Fibonacci Sequence?
The Geometric Fibonacci Sequence is a variation of the traditional Fibonacci Sequence where each term is the product of the previous two terms. It combines the mathematical beauty of the Fibonacci Sequence with a geometric progression.
What are the patterns and properties of the Geometric Fibonacci Sequence?
The Geometric Fibonacci Sequence exhibits fascinating patterns: every term is either a perfect square or a product of squares, and it converges to the Golden Ratio. It also displays a self-similarity property, where smaller subsequences replicate the overall pattern.
Are there references to the Geometric Fibonacci Sequence in ancient texts?
Ancient texts, such as the Vedas and the works of ancient Greek mathematicians, mention geometric progressions that bear similarities to the Geometric Fibonacci Sequence. These references suggest that ancient cultures were aware of this mathematical concept.
How is the Geometric Fibonacci Sequence connected to sacred geometry?
Sacred geometry, the study of geometric shapes and proportions in spiritual art and architecture, often incorporates the Golden Ratio. As the Geometric Fibonacci Sequence converges to the Golden Ratio, it is considered sacred and linked to the principles of divine design.
What ancient texts and symbols relate to the Geometric Fibonacci Sequence?
Ancient symbols, such as the spiral, have been associated with the Geometric Fibonacci Sequence due to its appearance in natural phenomena. Ancient texts like the Bhagavad Gita and the works of Plato mention geometric principles that align with the sequence.
How is the Geometric Fibonacci Sequence observed in nature?
Nature abounds with examples of the Geometric Fibonacci Sequence, from the arrangement of spirals in seashells and hurricanes to the branching patterns of trees and the distribution of leaves on a stem. These patterns reflect the inherent mathematical order in the natural world.
What are some modern applications of the Geometric Fibonacci Sequence?
The Geometric Fibonacci Sequence finds practical applications in many fields, such as computer science, data analysis, and algorithm design. It is also used in financial modeling, market analysis, and predicting stock market trends.
How does the Geometric Fibonacci Sequence help unravel mysteries?
By studying the Geometric Fibonacci Sequence, researchers have made discoveries and connections in various fields, ranging from archaeology and ancient civilizations to biological structures and DNA sequences. Its inherent patterns help unravel mysteries and reveal hidden relationships.








